無料ダウンロード 割り算��商と余り 高校 260771-割り��の商と余り 高校

整式を商 あまりで表現する 高校数学の知識庫
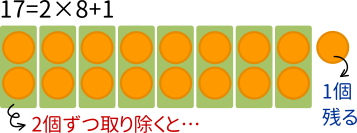
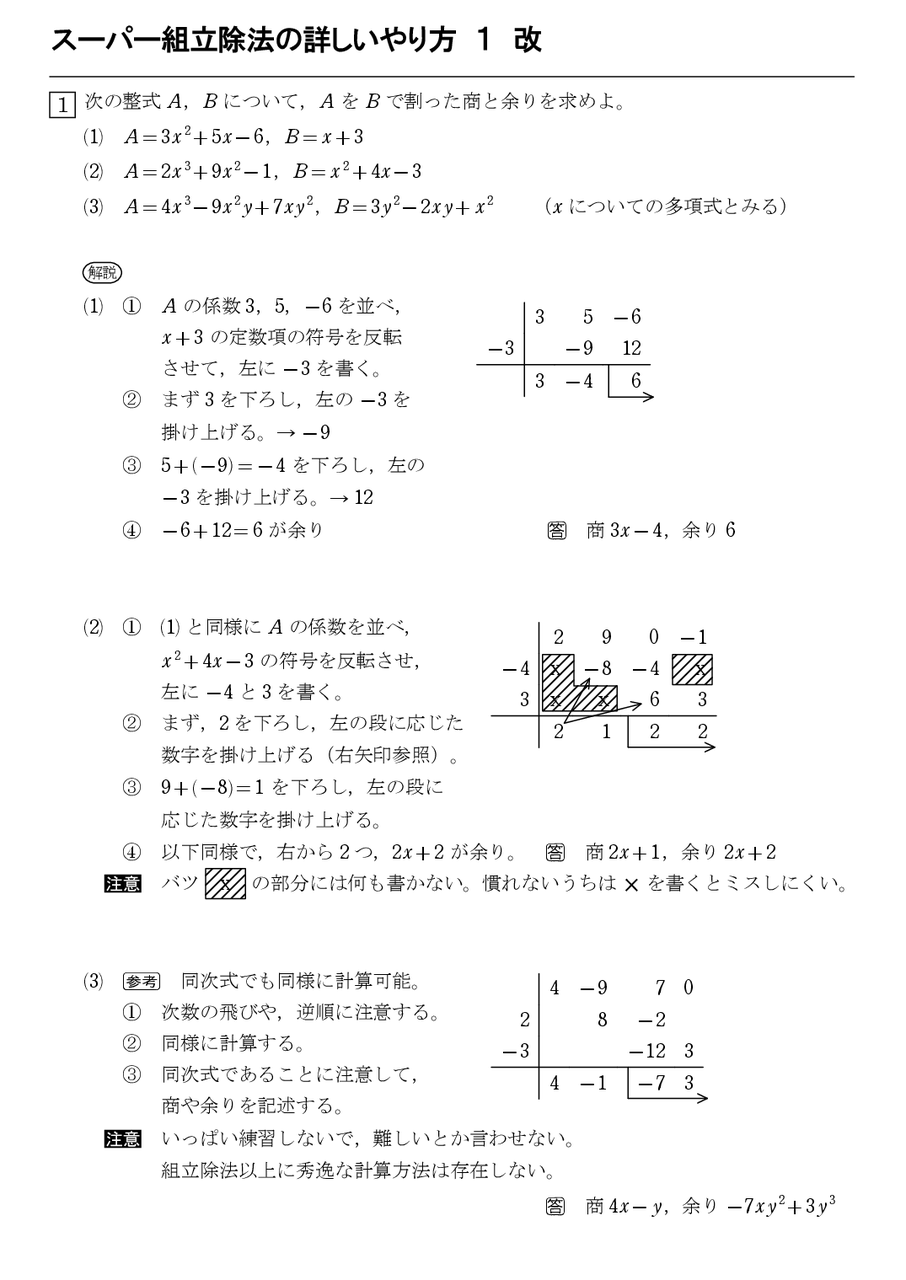
上に商の係数が並び,下に余りの係数が並ぶ。 この場合,商の係数は順番に 1,3 1,3 なので Q (x)=x3 Q(x) = x 3 , 余りの係数は順番に 1,7 −1,−7 なので R (x)=x7 R(x) = −x− 7 と分かります。 二つの方法の比較,例題 慣れたら方法2(筆算)の方がかなり早いですが,割り算の意味,構造は方法1(恒等式)の方が分かりやすいです。 B (x) B(x) が一次式(特に一次の係数が1)のとき 掛け算が 元の数とかける数から 「 結果 」を求めるのに対し、割り算は 元の数と結果から 「 かける数 」を求めるものです。 やっていることは掛け算です。 ただ「 着眼点が違う 」だけです。 なので「 割られる数 ÷ 割る数 = 商 余り 」→「 割られる数 = 割る数 × 商 + 余り 」と変形できるのです。 例えば「 17 ÷ 3 」なら「 17 = 3 × + 」なので、九九の 3 の段の知識 ( 掛け算 )が必要に
割り算の商と余り 高校
割り算の商と余り 高校-8月 02, 21 数学Ⅲ・C 公式集 <関数と極限> ① 分数関数 ax b cx b y = のとき割り算の商と余りを利用して x q r y p= と変形できる。このときグラフは、漸近線が、 x=q,y=pの直角双曲線になる。 ② 無理関数すると以下のように余りが求められます。 計算された値を元に、オートフィル機能で全体を計算しましょう。これで、すべての割り算における余りが求められました。 関連記事 オートフィル機能の使い方 商と余りを合わせて表示する方法

多項式の割り算の二通りの計算方法と例題 高校数学の美しい物語
19整数の割り算と商、余り ・整数の割り算の商と余り(マイナスの割り算も)数A ・2数の和差積と余り:数A ・準備整数の文字での表し方 ・数A倍数や余りの証明 ・数A余りによる整数の分類 ・数A連続する整数の積と証明 ・数ADivision a÷b (1) a÷b =c⋯d (2) a =b×cd Quotient c Remainder d D i v i s i o n a ÷ b ( 1) a ÷ b = c ⋯ d ( 2) a = b × c d Q u o t i e n t c R e m a i n d e r d お客様の声 アンケート投稿 よくある質問 リ小学校の算数でも学習した内容になるけど、 16÷5=3 あまり1 と表現するとき、 割り算して出てきた答え 「3」を 「商」 、そして「1」を 「余り」 と言ったよね。 この数式を、算数 数学にレベルアップさせると、次のような表し方になるんだ。
考え方 上の説明ではわかりづらいですが,とりあえず基本的な問題を解くために覚える必要があるのは次の2つです. 1 aをbで割ったときの商qと余りrを使って等式a=bqrの形が作れる 2 a=bqr (0≦r<b)が成り立っているとき,aをbで割ったときの商がq,余りがrとなる (割られる数)=(割る数)×(商)(余り)となることを簡単な例で説明してみます.たとえば,26この3つのコマンドは,整数に対しても使うことができて,割り算の商や余りを求めることができます。Division は計算結果がリスト形式で出力され,Div と Mod は整式で出力されるという違いがあります。スクリプトを書くときには注意が必要になります。 これを 除法の原理 という。 ① ② この式における を、をで割ったときの商と呼び、をその余り(剰余)と呼ぶ。 というのは次数をかっこつけて表現しただけの数学機構であり、例えば f (x) = x^2 8に対しては になるという、それだけの話だ。 ちなみに「整式」は 多項式 と単項式の総称だが、受験数学においては十中八九 多項式 を考えることになる
割り算の商と余り 高校のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 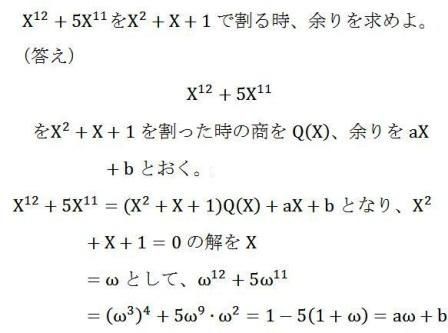 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
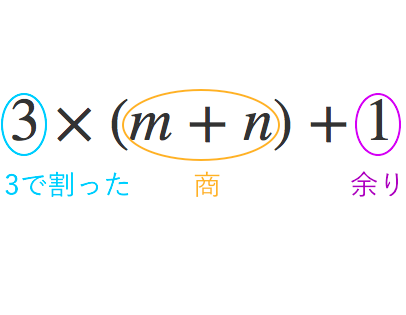 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 | 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
 式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |  式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集 |
例えば、を3で割ると\ =3\times(6)2 \なので、商は $6$ で余りは $2$ です。を3で割ると\ =3\times71 \なので、商は $7$ で余りは $1$ となります。 なお、割る数を $0$ にすると、商が1つに定まりません。そのため、通常は、0で割ることは考えません。割り算について成り立つ等式(商と余りの関係,割り算の原理) 問題 第1問 / 全3問中 採点する 次の問題 解説 ※定数項や1次式,2次式など単項式や多項式で表わされる式を整式という. 要約 整式 a を 整式 b で割ると,商が q 余りが r になるとき, (1) a ÷ b=q r ⇔ a=bqr (2) 余り
Incoming Term: 割り算の商と余り 高校,
コメント
コメントを投稿